More actions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Infobox DS Homebrews | {{Infobox DS Homebrews | ||
| title | |title=Mandelbrot Fractal (Fractal Junkie) | ||
| image | |image=[[File:Mandelbrotfractds.png]] | ||
| type | |description=A fractal browser. | ||
| version | |author=TheMagnitude | ||
| license | |lastupdated=2008/04/27 | ||
| | |type=Mathematics | ||
|version=2.0 | |||
| website | |license=Mixed | ||
|download=https://dlhb.gamebrew.org/dshomebrew/mandelbrotfractal.7z | |||
|website=http://themagnitude.co.uk/index.php?cmd=apps&id=7 | |||
}} | }} | ||
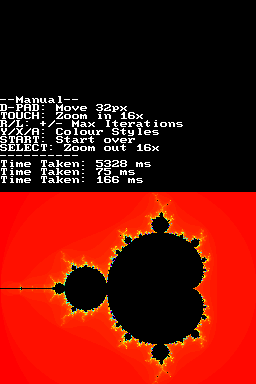
The Mandelbrot set is a set of points in the complex plane, the boundary of which forms a fractal. | The Mandelbrot set is a set of points in the complex plane, the boundary of which forms a fractal. | ||
Revision as of 02:19, 28 October 2021
| Mandelbrot Fractal (Fractal Junkie) | |
|---|---|
| File:Mandelbrotfractds.png | |
| General | |
| Author | TheMagnitude |
| Type | Mathematics |
| Version | 2.0 |
| License | Mixed |
| Last Updated | 2008/04/27 |
| Links | |
| Download | |
| Website | |
The Mandelbrot set is a set of points in the complex plane, the boundary of which forms a fractal.
When computed and graphed on the complex plane, the Mandelbrot Set is seen to have an elaborate boundary, which does not simplify at any given magnification. This qualifies the boundary as a fractal.
The Mandelbrot set has become popular outside mathematics both for its aesthetic appeal and for being a complicated structure arising from a simple definition. Benoît Mandelbrot and others worked hard to communicate this area of mathematics to the public.
Features
- 64bit accuracy.
- Mandelbrot set.
- Custom Julia sets (this includes Fatou Dust).
- 7 Colour Palletes (Cycle without redrawing).
- 3 Colour Styles (Cycle without redrawing).
- Successive Refinement Rendering.
- Only calculates unknown pixels when moving.
- Draw with the stylus a new view from any two points on the screen to zoom to that view.
Controls
D-Pad - Move 32px
Stylus - Draw a new view
R/L - +/- Iterations
A - Colour Styles
B - Colour Pallets
X - Toggle precise rendering
Y - Toggle Julia set mode
Start - Start over
Select - Goto previous image
Screenshots
Changelog
2.0
- Much much further zoom, can zoom up to 2^40 now.
- 3 Colour mapping functions.
- Gradient of 6 colours.
- Increase/Decrease iterations.
- Zoom out.
External links
- Author's website - http://themagnitude.co.uk/index.php?cmd=apps&id=7
